Свойство центральной симметричности
| Сайт: | Открытый электронный университет |
| Курс: | Физика для Менеджеров |
| Книга: | Свойство центральной симметричности |
| Напечатано:: | Гость |
| Дата: | пятница, 9 января 2026, 17:49 |
Описание
Ключевую роль играет свойство центральной симметричности гиперкуба и фигуры из трёх вложенных гиперкубов. Как это использовать в доказательстве Великой теоремы?
1. Послойное тождество
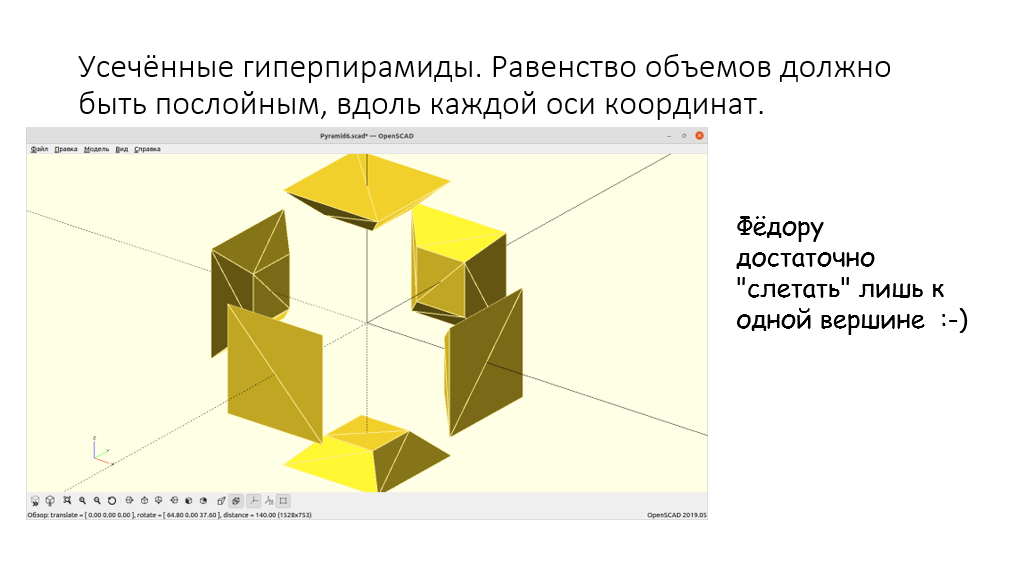
Рис 6. Гиперкуб размерности 3, рассеченный на гиперпирамиды. Показан лишь один слой.
Другими словами, в силу свойства центральной симметричности фигуры можно сфокусировать внимание на исследовании слоёв лишь одной из 2n гиперпирамид (треугольника для случая n = 2).
В силу одинаковой структуры всех слоёв в гиперкубе, сосредоточим внимание на элементе mn-k1k -
биноминальные коэффициенты во всех слоях одни и те же, и поэтому они
сокращаются при операциях сравнения, сложения, вычитания объёмов слоёв,
не играя принципиальной роли. Как было установлено выше из принципа
соответствия, размерность элемента dim( mn-k1k )
= n–k. Сравнение элементов разных слоёв должно происходить строго с
соблюдением этой размерности, иначе при изменении масштаба тожество
нарушится.
2. Особый двумерный случай
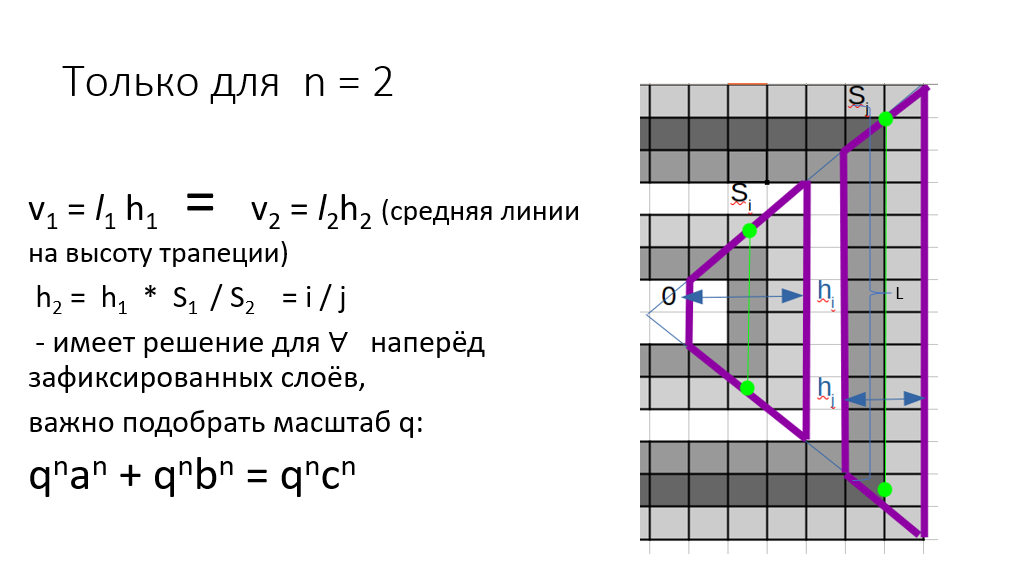
Рисунок 7 Любые два множества последовательно следующих слоёв S в двумерном пространстве имеют соизмеримые объемы (площади).
При n = 2 сравнение происходит лишь по элементам размерности равной единице - рёбрам. Легко добиться равенства мощностей |{ . . . Si . . . }| = |{ . . . Sj ... }| для любых ∀ слоёв i, j, что означает количественное равенство гиперкубиков в обоих множествах. Но в общем случае сопоставление одного или множества слоёв из подмножеств точек многомерного пространства cn - bn с объёмом множества слоёв в малом гиперкубе an равносильно нахождению решения системы из n-1 уравнений:
jn-1 = kn-1 + (k-1)n-1 + (k-2)n-1 … как минимум два слагаемых или более.
Система из n-1 уравнений (4)
jn-2 = kn-2 + (k-1)n-2 + (k-2)n-2… как минимум два слагаемых или более.
. . . . . . . . . . .
Здесь имеется в виду, что объём слоя Sj должен быть равен сумме объемов слоёв в силу несжимаемости объёма:
Sk, Sk-1, Sk-2 . . . . (хотя бы два и более слагаемых) следующих последовательно в малом гиперкубе an в силу свойства непрерывности гиперкуба и необходимости полного заполнения слоёв элементарными гиперкубиками 1n. Иначе возникнут пустоты - дефект фигуры, нарушатся её свойства центральной симметричности и непрерывности этого множества точек в Rn.
Эта система уравнений продолжается до вторых и первых степеней, т.е. двумерных граней и одномерных ребер. Такая система не разрешима при n > 2 не только в целых, но и в действительных числах R.
2.1. Почему эта система не разрешима?
Эта
система уравнений продолжается до
вторых и первых степеней, т.е. двумерных
граней и одномерных ребер. Такая система
не разрешима при n > 2 не только в целых,
но и в действительных числах R.
Для понимания этого достаточно
сосредоточить внимание на последних
двух уравнениях в системе:
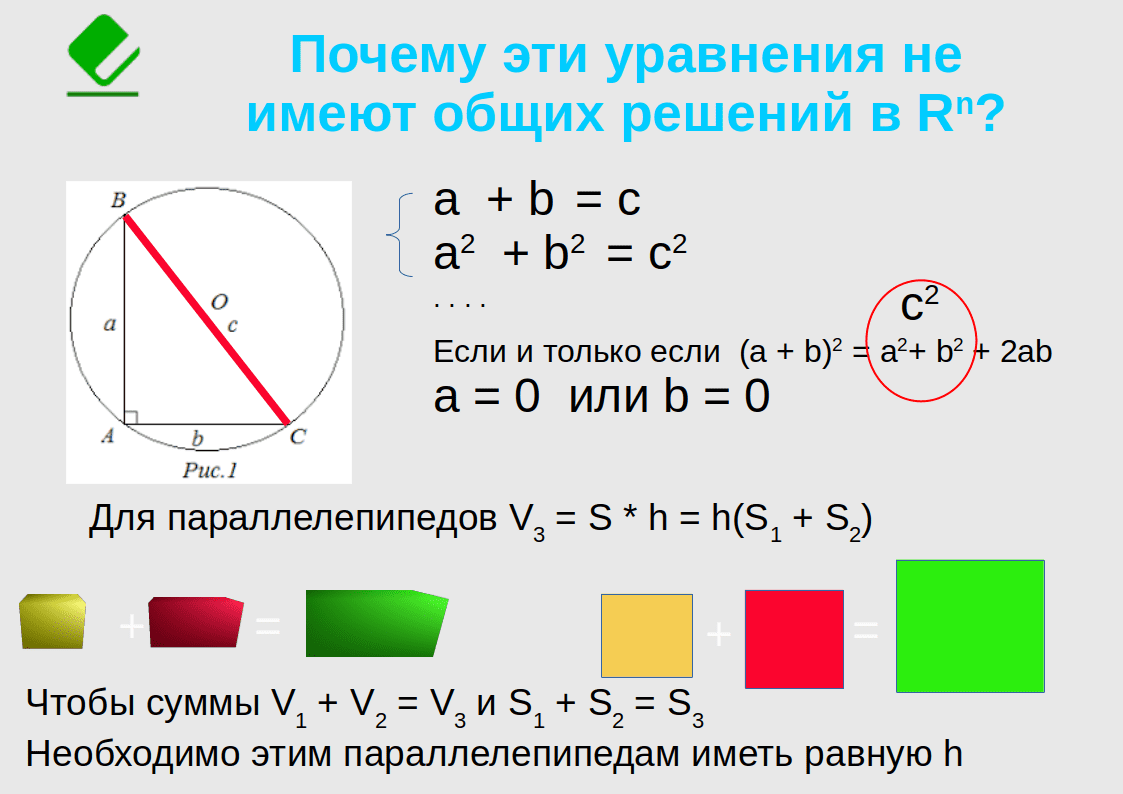
если сумма
катетов прямоугольного треугольника
равна гипотенузе и одновременно сумма
квадратов катетов равна квадрату
гипотенузы, то длина хотя бы один из
катетов с необходимостью должен быть
равен нулю: c2
= (a
+b)2
= a2
+ b2
+ 2ab => a = 0 V b = 0 (V - знак дизъюнкции,
логическое ИЛИ). Случай многих слагаемых
справа каждого уравнения в системе
можно свести лишь в двум, если оперировать
не в целых, а в действительных числах
R. Между тем, мы исключаем в нашем
рассмотрении гиперкубы с нулевым
размером ребра. Налицо противоречие, а
следовательно система уравнений (4) не
разрешима даже в действительных числах
R, при n > 2.