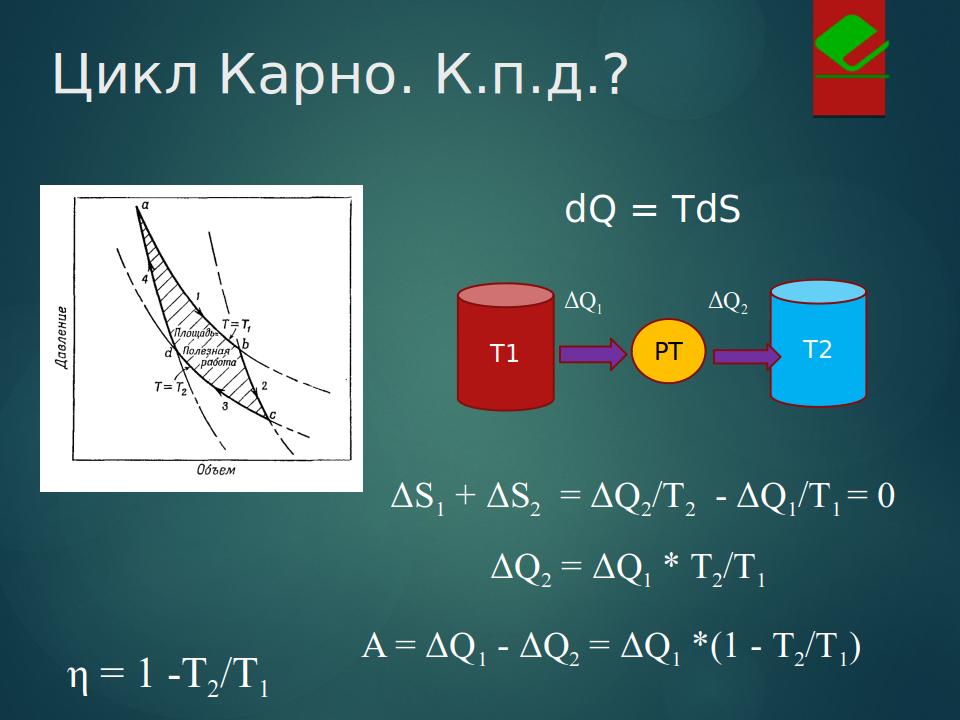
Цикл идеальной машины Сади Карно - окружен по контуру двумя изотермами (pV = RT) и двумя адиабатами (pV^γ = const). Коэфф. полезного действия к.п.д. - это отношение площади этого цикла ⌡pdV к затратам тепловой энергии на один проход по контуру. Ричард Фейнман в томе 4 свои Лекций, считает интеграл только по изотермам, игнорируя адиабаты. Почему? Вопрос № 2: можно ли опираясь на понятие энтропии взять этот интеграл, не интегрируя?
Отвечаю на поставленный вопрос, который кажется сначала трудным, но . . . Итак, участки двух адиабат (pV^γ = const ) соответствуют изменениям на диаграмме Давление - Объём, без теплообмена: dQ = dU -pdV = 0. Это значит, что работа dA =pdV совершается за счет внутренней энергии газа dU. В свою очередь внутренняя энергия идеального газа зависит только от абсолютной температуры T. Цикл Карно ограничивается сверху и снизу T нагревателя и T охладителя соответственно. Итак участки двух адиабат слева и справа вносят / забирают одно и то же значение: газовая постоянная умножить на . . . R (ΔT - ΔT). Всё это обнуляется. Что касается расчета КПД без интегрирования, то это вытекает из определения энтропии ΔS = ΔQ /T. Поскольку идеальная машина построена без тепловых потерь и трения (это идеал), она обратима. Следовательно, по итогам работы цикла энтропия не увеличится, а останется прежней и ΔQ1 /T1 = ΔQ2 /T1. Отсюда легко рассчитаться работу и КПД: A = ΔQ1 - ΔQ2 и далее как на рисунке. В результате интеграл взят без интегрирования!