Тематический план
-
 Когда СССР запустил спутник в космос, президент США сказал: ребята, учите физику, иначе придется учить русский язык! За полвека ситуация изменилась до неузнаваемоти *. В США курс по физике изучают даже менеджеры. Почему? Потому, что знание основ физики необходимо для принятия управленческих решений. Авария на Чернобыльской АЭС и Саяно-Шушенской ГЭС — это наглядные результаты некомпетентных действий.
Когда СССР запустил спутник в космос, президент США сказал: ребята, учите физику, иначе придется учить русский язык! За полвека ситуация изменилась до неузнаваемоти *. В США курс по физике изучают даже менеджеры. Почему? Потому, что знание основ физики необходимо для принятия управленческих решений. Авария на Чернобыльской АЭС и Саяно-Шушенской ГЭС — это наглядные результаты некомпетентных действий.-
ФорумГлавные новости и объявления. Подпишитесь, чтобы оставаться в курсе новостей!
-
 Это видео-инструкции, пошаговое описание учебных процессов. Электронный платформы позволяют организовать групповую работу на качественно новом уровне. Синергийный эффект достигается за счет создания разделяемого отвечающего запросам участников мультимедийного контента, который становится легко доступным, свободно транслируется по каналам связи без использования профессионального специализированного оборудования и привлечения квалифицированных специалистов.
Это видео-инструкции, пошаговое описание учебных процессов. Электронный платформы позволяют организовать групповую работу на качественно новом уровне. Синергийный эффект достигается за счет создания разделяемого отвечающего запросам участников мультимедийного контента, который становится легко доступным, свободно транслируется по каналам связи без использования профессионального специализированного оборудования и привлечения квалифицированных специалистов.
-
-
Основы дифференциального и интегрального исчисления важно для понимания базовых принципов физики и не только физики, а любых динамических процессов.
-
Функции. Интеграл. Производная - се эти понятия пришли в математику из потребностей решения задач Астрономии и физики. Поэтому тему лучше раскрыть с позиции физики.
-
-
Механика - основной раздел общей физики
-
Книга
Основы механики для школьников и их родителей
-
Книга
Публикации о международной гонке космических технологий
-
Основные физические данные о планетах Солнечной системы по данным НАСА
-
Объясните явление прецессии на примере демонстрации этого опыта
-
 Программа на языке Java для моделирование колебаний в механических системах. Подходит для любых операционных систем.
Программа на языке Java для моделирование колебаний в механических системах. Подходит для любых операционных систем.
-
-
Молекулярная физика, теплофизика помогает понять работу с жидкостями и газами. Здесь же основы термодинамики, первый и второй законы, энтропия, идеальный газ, барометрическая формула Больцмана и распределение Максвелла.
-
Здесь можно обсудить занятия
-
Распределение Максвелла. Моделирование опыта
-
-
Закон Кулона, электрический потенциал Энергия поля. Электрический дипольный момент. Физика.
-
-
Необычайная красота и лаконичность формулировки Великой теоремы Ферма заставляют искать её наглядное решение. Попробуем рассмотреть эту теорему Ферма с позиции физики и геометрии. Что если озарение, о котором упоминал Пьер де Ферма в 1637 г. на полях Арифметики Диофанта: “Я нашёл воистину чудесное доказательство!” было не фигурой речи, а результатом творческого воображения?
-
 Великую теорему Ферма, без преувеличения, следует отнести к жемчужинам научного знания, поскольку её можно рассматривать с позиции теории чисел, геометрии, алгебры, комбинаторики, теория множеств, информатики, физики, логики и философии. Именно на примере этой теоремы в полной мере можно раскрыть преимущества конвергенции научных знаний в сравнении с узкоспециализированными методами исследований.
Великую теорему Ферма, без преувеличения, следует отнести к жемчужинам научного знания, поскольку её можно рассматривать с позиции теории чисел, геометрии, алгебры, комбинаторики, теория множеств, информатики, физики, логики и философии. Именно на примере этой теоремы в полной мере можно раскрыть преимущества конвергенции научных знаний в сравнении с узкоспециализированными методами исследований. -
Проведенное исследование показало, что последовательное применение основных принципов физики, геометрии, алгебры, теории множеств и информатики являются залогом успеха.
-
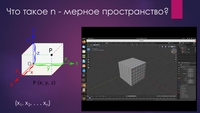
 В результате этого эксперимента учащиеся получат представление о многомерном пространстве действительных чисел Rn, о гиперкубе, описываемом формулой an, а также о гиперплоскости - множестве точек (x1,x2, . . . xn) ∈ Rn , где xi = const для некоторой оси, т.е индекса i - целого ≤ n.
В результате этого эксперимента учащиеся получат представление о многомерном пространстве действительных чисел Rn, о гиперкубе, описываемом формулой an, а также о гиперплоскости - множестве точек (x1,x2, . . . xn) ∈ Rn , где xi = const для некоторой оси, т.е индекса i - целого ≤ n. -
Страница
Как строго математически определить понятие слоя? Сначала мы выберем более удобное представление: гиперкубы с целочисленными рёбрами 1,2, 3, . . .i, полученные на основе ряда натуральных чисел,
-
Согласны ли Вы с утверждением, что для рассматриваемой нами фигуры из трёх гиперкубов слой имеет размерность на единицу меньше, чем объём, охватываемый им? Обсудите аргументы и контраргументы.
-
Ключевую роль играет свойство центральной симметричности гиперкуба и фигуры из трёх вложенных гиперкубов. Как это использовать в доказательстве Великой теоремы?
-
Задание
Полезно убедиться с учащимися в иррациональности √2, n√2 от противного, представив, что натуральные и взаимно простые p и q существуют, тогда ... ( что именно?)
Согласны ли Вы с утверждением: Каждый слой в фигуре из трёх вложенных гиперкубов является уникальным в том смысле, что Sj = Sk <=> j = k. Слои были бы подобны друг другу лишь при условии (каком?)
-
Познакомимся с основами теории множеств. М
 ножество, подмножество, пересечение, объединения и дополнение, разность множеств, Декартово произведение, а также наглядное представление перечисленного с помощью диаграмм Эйлера Венна позволяют дать строгое определение слою и гиперкубу
ножество, подмножество, пересечение, объединения и дополнение, разность множеств, Декартово произведение, а также наглядное представление перечисленного с помощью диаграмм Эйлера Венна позволяют дать строгое определение слою и гиперкубу -
Представим себе вписанные друг в друга гиперкубы с рёбрами, полученными из ряда последовательных натуральных чисел N1. Теорема Ферма эквивалентна высказыванию: в n-мерном пространстве целых чисел Zn невозможно вписать друг в друга три гиперкуба с ребрами a, b, c таким образом, чтобы мощности |A| = |C|
-
Доказательство теоремы Ферма сводится к вопросу: существует ли отношение эквивалентности G между разными слоями для исследуемой фигуры?
-
Форум
 Автор открытия обращался в ряд научных организаций по поводу Великой теоремы Ферма. Ответно Автор открытия получил критические замечания, касающиеся преимущественно оформления математического открытия приводим переписку, вкл. письма Эндрю Уайлсу,
Автор открытия обращался в ряд научных организаций по поводу Великой теоремы Ферма. Ответно Автор открытия получил критические замечания, касающиеся преимущественно оформления математического открытия приводим переписку, вкл. письма Эндрю Уайлсу, -
База данных
 Ориентироваться в большом количестве книг, презентаций, видео-клипов по темам занятий помогут электронный документооборот и база данных. Это не дублирование материала, а скорее удобная классификация в одной базе данных. Книги, плейлисты на видео-клипы и презентации - всё в одном месте!
Ориентироваться в большом количестве книг, презентаций, видео-клипов по темам занятий помогут электронный документооборот и база данных. Это не дублирование материала, а скорее удобная классификация в одной базе данных. Книги, плейлисты на видео-клипы и презентации - всё в одном месте! -
 В целях наглядности в этом фильме представлена анимация используемых для доказательства гиперкубов, пирамид и др. 3D фигур и в формате STL, которые можно импортировать в программы OpenSCAD, Blender или аналогичных, «повертеть руками» со всех ракурсов и распечатать на 3D принтере. Установите для этого кросс - платформенный инструмент OpenSCAD
В целях наглядности в этом фильме представлена анимация используемых для доказательства гиперкубов, пирамид и др. 3D фигур и в формате STL, которые можно импортировать в программы OpenSCAD, Blender или аналогичных, «повертеть руками» со всех ракурсов и распечатать на 3D принтере. Установите для этого кросс - платформенный инструмент OpenSCAD -
Доказательство Великой Теоремы Ферма в рисунках. Учащиеся разбиваются на группы, ищут доказательство совместно. Кто-то из групп сделает открытие, но даже если этого не произойдет, этот проект поможет развитию творческого воображения учащихся.
-
Подведение итогов. Великая Теорема Ферма. Парадоксы. Физика и философия.
-
Вы сможете пересказать это доказательство своим внукам и правнукам: настолько оно просто и очевидно.
-
 Если Вам понравился этот проект, то Вы можете заказать Гиперкуб деревянный трёхмерный на сборной подставке с доказательством Великой теоремы Ферма с помощью лазерной гравировки. Наглядное доказательство, которое на протяжении почти четырёх долгих столетий считалось невозможным. Изделие можно установить на рабочий стол или на полку. Отличный повод начать диалог с коллегами и друзьями, прикоснувшись к четырёхвековой истории поиска доказательства!
Если Вам понравился этот проект, то Вы можете заказать Гиперкуб деревянный трёхмерный на сборной подставке с доказательством Великой теоремы Ферма с помощью лазерной гравировки. Наглядное доказательство, которое на протяжении почти четырёх долгих столетий считалось невозможным. Изделие можно установить на рабочий стол или на полку. Отличный повод начать диалог с коллегами и друзьями, прикоснувшись к четырёхвековой истории поиска доказательства!
-
-
Квантовая механика врывается в нашу жизнь через квантовый компьютер и криптографию.
-
 Ожидается, что с помощью квантовых вычислений можно будет создавать модели городов и даже галактик,
оптимизировать транспортные потоки, моделировать молекулы ДНК и новые материалы, делать финансовые
прогнозы. Среди наиболее перспективных направлений — дешифровка и квантовая криптография, а также точная
навигация, не требующая использования GPS. (автор: Заур Мамедьяров)
Ожидается, что с помощью квантовых вычислений можно будет создавать модели городов и даже галактик,
оптимизировать транспортные потоки, моделировать молекулы ДНК и новые материалы, делать финансовые
прогнозы. Среди наиболее перспективных направлений — дешифровка и квантовая криптография, а также точная
навигация, не требующая использования GPS. (автор: Заур Мамедьяров)
-
-
Анкетирование, итоговое тестирование, аттестация по итогам обучения в зависимости от избранной образовательной программы.
-
Анкета
 Заполните пожалуйста эту анкету вдумчиво, анализируя каждый вопрос
Заполните пожалуйста эту анкету вдумчиво, анализируя каждый вопрос
-